KnowledgeShop

Learn & Share

Algorithms

Grokking Algorithms - http://adit.io/

Concepts

Big-O Notation

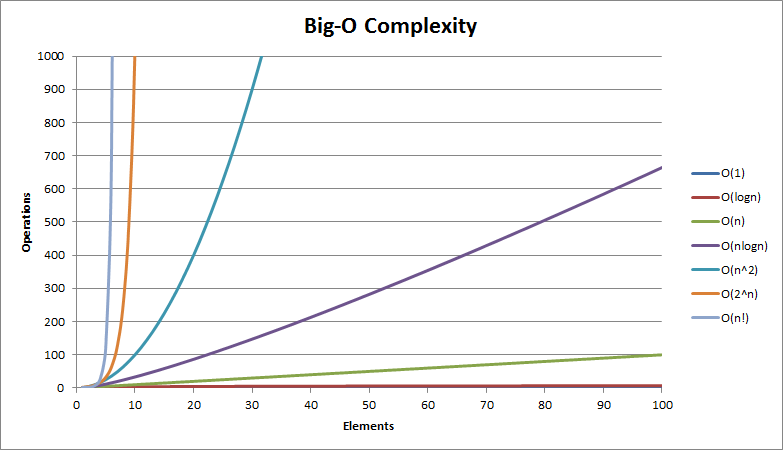
  • O(1)/Constant Complexity:
    • Constant. Irrespective of the size of the data set the algorithm will always take a constant time.
    • Example: HashMap.get() operation
  • O(log n)/Logarithmic Complexity:
    • Not as good as constant, but still pretty good. The time taken increases with the size of the data set, but not proportionately so. This means the algorithm takes longer per item on smaller datasets relative to larger ones. 1 item takes 1 second, 10 items takes 2 seconds, 100 items takes 3 seconds. This makes log n algorithms very scalable.
    • Example: Binary search
  • O(n)/Linear Complexity:
    • The larger the data set, the time taken grows proportionately. 1 item takes 1 second, 10 items takes 10 seconds, 100 items takes 100 seconds.
    • Example: To find an element T which is the last item in the LinkedList
  • O(n log n)/Linearithmetic Complexity:
    • A nice combination of the previous two. Normally there’s 2 parts to the sort, the first loop is O(n), the second is O(log n), combining to form O(n log n) 1 item takes 2 seconds, 10 items takes 12 seconds, 100 items takes 103 seconds.
    • Example: MergeSort. To explain why this is O(n log n) is a bit more complex. In the below example of 8 numbers, we have 3 levels of sorting:
      • 4 list sorts when the list sizes are 2
      • 2 list sorts when the list sizes are 4
      • 1 list sort when the list size is 8 Now consider if I were to double the number of elements to 16: this would only require one more level of sorting. This is a log n scale. However, on each level of sorting a total of n operations takes place (look at the red boxes in the diagram above). this results in (n * log n) operations.
  • O(n^2)/Polynomial or Quadratic Complexity:
    • Things are getting extra slow. 1 item takes 1 second, 10 items takes 100, 100 items takes 10000.
    • Example: Bubble Sort. If you need a reminder; we go through the list and compare each element with the one next to it, swapping the elements if they are out of order. At the end of the first iteration, we then start again from the beginning, with the caveat that we now know the last element is correct.
  • O(2^n)/Exponential Growth:
    • The algorithm takes twice as long for every new element added. 1 item takes 1 second, 10 items takes 1024 seconds, 100 items takes 1267650600228229401496703205376 seconds.
    • Example: Take for example trying to find combinations; imagine a list of 150 people and to find every combination of groupings; everyone by themselves, all of the groups of 2 people, all of the groups of 3 people etc. Using a simple program which takes each person and loops through the combinations, if I add one extra person then it’s going to increase the processing time exponentially. Every new element will double processing time.
  • Informal Introduction to BigO notation

How to find Big-O in interviews?

Break down the loops and processing.

  • Does it have to go through the entire list? There will be an n in there somewhere.
  • Does the algorithms processing time increase at a slower rate than the size of the data set? Then there’s probably a log n in there.
  • Are there nested loops? You’re probably looking at n^2 or n^3.
  • Is access time constant irrelevant of the size of the dataset? Then, O(1)

​ ## Proof by induction and contradiction

​An online algorithm that requires only constant space and runs in linear time is just about as good as possible.

Data Structures

Arrays

Strings

Linked Lists

Trees

Stacks

Queues

Algorithms

Searching

  • Binary Search
    • Binary Search in an array
    • Binary search matrix - pg 37
    • Binary search in partially sorted array (HarryHe pg 89 - unable to follow)
    • Minimum k numbers in an array - pg 191

Sorting

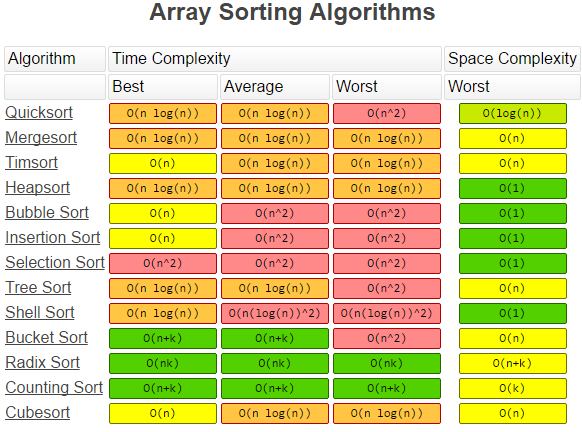
  • Array Sorting
  • String sorting
    • Counting sort or key-index counting (Sedgewick pg 703)
  • List sorting
    • ….

Heap sort visualization - http://www2.hawaii.edu/~copley/665/HSApplet.html

Backtracking

Bitwise Operations

  • AND (&)
    • 0 & 0 = 0
    • 1 & 0 = 0
    • 0 & 1 = 0
    • 1 & 1 = 1
  • OR (|)
    • 0 | 0 = 0
    • 1 | 0 = 1
    • 0 | 1 = 1
    • 1 | 1 = 1
  • XOR(^)
    • 0 ^ 0 = 0
    • 1 ^ 0 = 1
    • 0 ^ 1 = 1
    • 1 ^ 1 = 0
  • NOT (~)
    • ~0 = 1
    • ~0 = 0
  • Left Shift (<<)
    • 00001010 << 2 = 00101000
    • 10001010 << 3 = 01010000
  • Right Shift (>>)
    • 00001010 >> 2 = 00000010
    • 10001010 >> 3 = 11110001
  • Unsigned Right Shift (>>>)
    • 00001010 >>> 2 = 00000010
    • 10001010 >>> 3 = 00010001

Searching

  • Search types
    • exact search
    • range search
  • Search algorithm types
    • Sequential
    • Direct access (hashing)
    • Tree indexing methods
  • Binary Search
  • Dictionary/Interlpolation Search
  • Quadratic Binary Search

Hashing

  • Hashing Functions
    • Perfect hashing
    • Consistent Hashing or Hash Ring (used for building distributed caches, data sharding. Many NoSQL databases uses this including Voldemort, Amazon Dynamo, Couchdb, etc)
  • Collision Resolution Policy
    • Open Hashing/Separate Chaining
    • Closed Hashing / Open Addressing
      • Bucket Hashing
      • Linear Probing

Cons

Dynamic Programming

Greedy Algorithms

Reference

  • Idiot’s guide to BigO
  • bigocheatsheet.com
  • Books
    • Algorithms 4th Edition - Robert Sedgewick and Kevin Wayne
    • Algorithms in a Nutshell
    • ACE the programming interview
    • Coding Interview - Harry He
    • ​Data structures and algorithm analysis in Java